四川公考网行测技巧:数量关系一元二次函数求极值
行测考点范围很广,一般包括政治、法律、经济、人文、地理、科技、生活等方面,需要小伙伴们长时间不间断的积累。四川公务员考试网温馨提示考生阅读下文,相信能给考生带来一定的帮助。更多四川公务员考试复习技巧详见:2023年四川公务员考试教程(点击订购)。
一、什么是一元二次函数?
一元二次函数的基本表示形式为y=ax+bx+c(a≠0)。其图像是一条对称轴与y轴平行或重合于y轴的抛物线。当a>0时,函数图像开口向上,此时y有最小值;当a<0时,函数图像开口向下,此时y有最大值。
二、一元二次函数极值的求解方法
方法一:利用一元二次函数顶点公式求解
对于一元二次函数y=ax+bx+c(a≠0),其顶点坐标为 也就是当
也就是当
 也就是当
也就是当
方法二:利用“和定、差小、积大”求解
“和定、差小、积大”是指若两个式子的和为定值,两个式子间的差越小(最小为0),则两个式子的乘积越大。
下面我们通过两个例题来看一下这两种方法在解题时应该如何运用:
例1、某商品的进货单价为80元,销售单价为100元,每天可售出120件。已知销售单价每降低1元,每天可多售出20件。若要实现该商品的销售利润最大化,则销售单价应降低的金额是:
A.5元
B.6元
C.7元
D.8元
【答案】C。解析:
方法一,设应降低x元,总利润为y元。则降低后的销售单价为(100-x)元,销量为(120+20x)件,进货单价为80元,则总利润y=(100-x-80)×(120+20x),整理可得y=-20x?+280x+2400,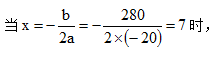 y能取到最大值,故本题选C。
y能取到最大值,故本题选C。
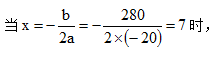 y能取到最大值,故本题选C。
y能取到最大值,故本题选C。 方法二,设应降低x元,总利润为y元。则降低后的销售单价为(100-x)元,销量为(120+20x)件,进货单价为80元,则总利润y=(100-x-80)×(120+20x)=20×(20-x)×(6+x),因为(20-x)+(6+x)=26,是定值,当且仅当20-x=6+x,即x=7时,y取最大值。故本题选C。
例2、某苗木公司准备出售一批苗木,如果每株以4元出售,可卖出20万株,若苗木单价每提高0.4元,就会少卖10000株。那么,在最佳定价的情况下,该公司最大收入是多少万元?
A.60
B.80
C.90
D.100
【答案】C。解析:
方法一,设苗木单价提高0.4x元,则可卖出(20-x)万株,此时收入为y万元,y=(4+0.4x)×(20-x),整理可得y=-0.4x?+4x+80,此时函数最大值为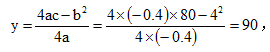 故本题选C。
故本题选C。
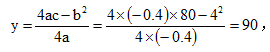 故本题选C。
故本题选C。 方法二,设苗木单价提高0.4x元,则可卖出(20-x)万株,此时收入为y万元,y=(4+0.4x)×(20-x)=0.4(10+x)×(20-x),因为(10+x)+(20-x)=30,是定值,故当且仅当10+x=20-x,即x=5时,y取最大值,收入最大为(4+0.4×5)×(20-5)=6×15=90万元。故本题选C。
通过上面两个例题,我们可以看到无论是采用一元二次函数的顶点公式还是采用“和定,差小,积大”的方法都可以解出题目。方法一需要我们将函数整理为一般式;方法二需要我们将函数整理成两式相乘,且两式未知数系数互为相反数的形式,之后再使两式满足“和定、差小”的条件。那么,对于方法各位考生可以选择适合自己的,只要通过练习,达到顺利解题的目的即可。
 更多四川公务员行测技巧与方法扫码获取
更多四川公务员行测技巧与方法扫码获取
四川公务员快速提分手册(点击订购)
上架啦!
快速掌握出题规律,提炼解题技巧,强化提升10%的解题时间

为助力考生直击快速上岸,配套还赠送模拟卷+课程+练习
 更多公务员行测技巧,扫码回复“咨询老师”
更多公务员行测技巧,扫码回复“咨询老师”


点击分享此信息:
 相关文章
相关文章


